Welcome to Catharina's web page

I wanted to start my web page with a picture taken at the "Görauer Anger", this is a place near the village I grew up . It is in Franconia, the northern part of Bavaria which is one of the 16 federal states of Germany.

I like to hike and near my hometown and especially around Nuremberg there are a lots of nice hiking trails. In the video you can see and example. It is a trail which guides you from brewery to brewery and you can tast lots of good franconian beer.

Maxwell's Equations

In my field of studies I had to study the Maxwell's Equations which describe the connection between electrical and magnetic fields and the electrical charge and the electric current under special constraints

\begin{align} \nabla \times \vec{\mathbf{B}} -\, \frac1c\, \frac{\partial\vec{\mathbf{E}}}{\partial t} & = \frac{4\pi}{c}\vec{\mathbf{j}} \\ \nabla \cdot \vec{\mathbf{E}} & = 4 \pi \rho \\ \nabla \times \vec{\mathbf{E}}\, +\, \frac1c\, \frac{\partial\vec{\mathbf{B}}}{\partial t} & = \vec{\mathbf{0}} \\ \nabla \cdot \vec{\mathbf{B}} & = 0 \end{align}

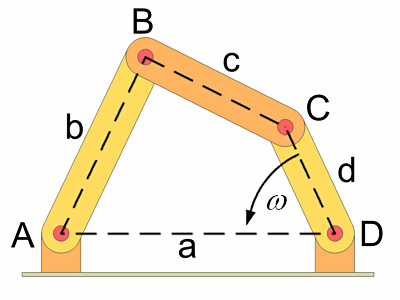
This is an extract from a Matlab script for the symbolic calculation for a kinematic problem like this:

symboliccalculation
clear
close all
clc

% Declare symbolic variables
syms xa ya thitaa xb yb thitab xc yc thitac xd yd real
syms xap yap thitaap xbp ybp thitabp xcp ycp thitacp xdp ydp real
syms L1 L2 L3 L4 L5 w t thitaA0 beta real

% phi-Matrix with the former declared parameters
phi = [ -thitaA0+thitaa-w*t;
     xa-L2/2*cos(thitaa);
     ya-L2/2*sin(thitaa);
     xb-xa-L2/2*cos(thitaa)-L3/2*cos(thitab);
     yb-ya-

L2/2*sin(thitaa)-L3/2*sin(thitab);
     xc-xb-L3/2*cos(thitab)-L4/2*cos(thitac);
     yc-yb-L3/2*sin(thitab)-L4/2*sin(thitac);
     L1-xc-

L4/2*cos(thitac);
     0-yc-L4/2*sin(thitac);
     xd-xa-L2/2*cos(thitaa)-L5*cos((thitab+beta));
     yd-ya-L2/2*sin(thitaa)-L5*sin((thitab

+beta))];

q = [xa ya thitaa xb yb thitab xc yc thitac xd yd]';

phiq = jacobian(phi,q); % Calculates phit by deriviting 

phi with q
phit = diff(phi,t); % Calculates phit by deriviting phi with t

qp = [xap yap thitaap xbp ybp 

thitabp xcp ycp thitacp xdp ydp]';
phitt = diff(phit,t);
phiqt = diff(phiq,t);
gammma = [jacobian(phiq*qp,q)*qp+2*phiqt*qp+phitt];


Published with MATLAB® R2013a