Catharina's page

The task was to creat a web page which includes multimedia. Which could be a picture (for example of home, Franconia):

In my field of studies I had to study the Maxwell's equations which discribe the connection between electrikal and magnetic fields and the elektrical charge and the electric current under special constraints

Maxwell's Equations

\begin{align} \nabla \times \vec{\mathbf{B}} -\, \frac1c\, \frac{\partial\vec{\mathbf{E}}}{\partial t} & = \frac{4\pi}{c}\vec{\mathbf{j}} \\ \nabla \cdot \vec{\mathbf{E}} & = 4 \pi \rho \\ \nabla \times \vec{\mathbf{E}}\, +\, \frac1c\, \frac{\partial\vec{\mathbf{B}}}{\partial t} & = \vec{\mathbf{0}} \\ \nabla \cdot \vec{\mathbf{B}} & = 0 \end{align}

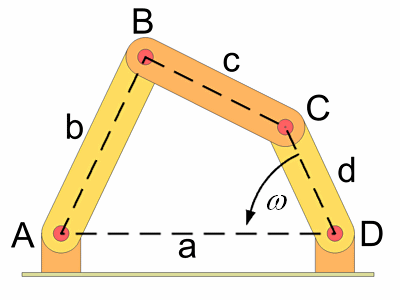
This an extract from a Matlab script for the symbolic calculation for a kinematic problem like this:

clear
close all
clc

% Declare symbolic variables
syms xa ya thitaa xb yb thitab xc yc thitac xd yd real
syms xap yap thitaap xbp ybp thitabp xcp ycp thitacp xdp ydp real
syms L1 L2 L3 L4 L5 w t thitaA0 beta real

% phi-Matrix with the former declared parameters
phi = [ -thitaA0+thitaa-w*t;
     xa-L2/2*cos(thitaa);
     ya-L2/2*sin(thitaa);
     xb-xa-L2/2*cos(thitaa)-L3/2*cos(thitab);
     yb-ya-L2/2*sin(thitaa)-L3/2*sin(thitab);
     xc-xb-L3/2*cos(thitab)-L4/2*cos(thitac);
     yc-yb-L3/2*sin(thitab)-L4/2*sin(thitac);
     L1-xc-L4/2*cos(thitac);
     0-yc-L4/2*sin(thitac);
     xd-xa-L2/2*cos(thitaa)-L5*cos((thitab+beta));
     yd-ya-L2/2*sin(thitaa)-L5*sin((thitab+beta))];

q = [xa ya thitaa xb yb thitab xc yc thitac xd yd]';

phiq = jacobian(phi,q); % Calculates phit by deriviting phi with q
phit = diff(phi,t); % Calculates phit by deriviting phi with t

qp = [xap yap thitaap xbp ybp thitabp xcp ycp thitacp xdp ydp]';
phitt = diff(phit,t);
phiqt = diff(phiq,t);
gammma = [jacobian(phiq*qp,q)*qp+2*phiqt*qp+phitt];

Welcome to Catharina's web page

Maxwell's Equations